Hashing
Hashing adalah teknik pada Data Strucuture yang digunakan untuk memetakan nilai yang diberikan dengan kunci tertentu untuk akses elemen yang lebih cepat. Misalkan fungsi hash H(x) memetakan nilai x pada indeks x% 10 dalam sebuah array. Sebagai contoh jika daftar nilai adalah [11,12,13,14,15] itu akan disimpan di posisi {1,2,3,4,5} masing-masing dalam array atau tabel hash.
Hash Function pada Data Structure:
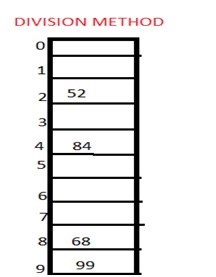
1. Division Method
Dalam hal ini fungsi hash tergantung pada sisa pembagian. Sebagai contoh, 52,68,99,84 harus ditempatkan di tabel hash dan mari kita ambil ukuran tabel adalah 10. Lalu,
Hash Function pada Data Structure:
1. Division Method
Dalam hal ini fungsi hash tergantung pada sisa pembagian. Sebagai contoh, 52,68,99,84 harus ditempatkan di tabel hash dan mari kita ambil ukuran tabel adalah 10. Lalu,
(key)=record% table size.
2=52%10
8=68%10
9=99%10
4=84%10
8=68%10
9=99%10
4=84%10
2. Mid Square Method
Dalam metode ini pertama kunci kuadrat dan kemudian bagian tengah hasilnya diambil sebagai indeks. Sebagai contoh, pertimbangkan bahwa jika kita ingin menempatkan catatan 3101 dan ukuran tabel adalah 1000. Jadi 3101 * 3101 = 9616201 yaitu h (3101) = 162 (tengah 3 digit)
3. Digit Folding Method
Dalam metode ini kunci dibagi menjadi bagian yang terpisah dan dengan menggunakan beberapa operasi sederhana bagian ini digabungkan untuk menghasilkan kunci hash. Sebagai contoh, perhatikan catatan 12465512 maka akan dibagi menjadi beberapa bagian yaitu 124, 655, 12. Setelah membagi bagian-bagian menggabungkan bagian-bagian ini dengan menambahkannya.
H(key)=124+655+12
=791
Collision
Karena fungsi hash memberi kita angka kecil untuk kunci yang merupakan bilangan bulat besar atau string, ada kemungkinan bahwa dua kunci menghasilkan nilai yang sama. Situasi di mana peta kunci yang baru dimasukkan ke slot yang sudah ditempati di tabel hash disebut tabrakan dan harus ditangani menggunakan beberapa teknik penanganan Collision.
Ada dua teknik dalam menangani Collision, yaitu:
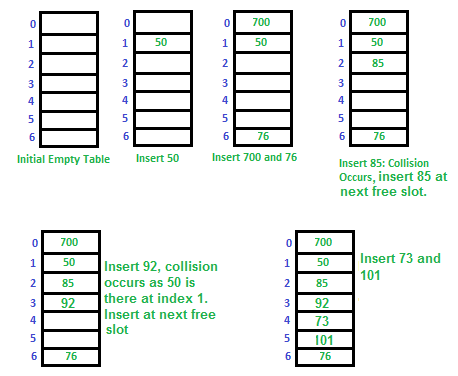
1. Linear Probing
Dalam linear probing, kita mencari secara linear slot berikutnya. Sebagai contoh, kesenjangan khas antara dua probe adalah 1 seperti diambil dalam contoh di bawah ini juga.
hash(x) menjadi indeks slot dihitung menggunakan fungsi hash dan S menjadi ukuran tabel
If slot hash(x) % S is full, then we try (hash(x) + 1) % S If (hash(x) + 1) % S is also full, then we try (hash(x) + 2) % S If (hash(x) + 2) % S is also full, then we try (hash(x) + 3) % S
Kita anggap fungsi hash sederhana sebagai "key mod 7" dan urutan tombol sebagai 50, 700, 76, 85, 92, 73, 101.
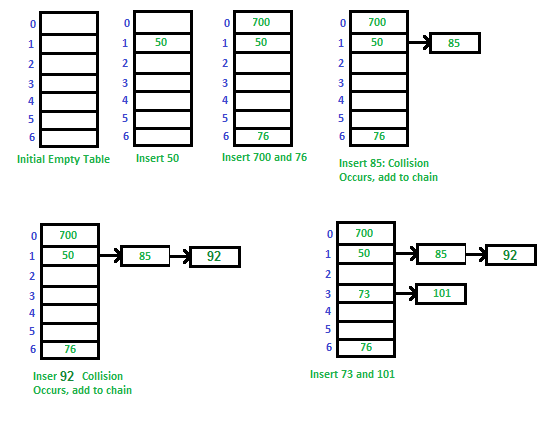
2. Chaining
Fungsi Chaining adalah untuk membuat setiap sel tabel hash menunjuk ke daftar catatan terkait yang memiliki nilai fungsi hash yang sama.
Kita anggap fungsi hash sederhana sebagai "key mod 7" dan urutan tombol sebagai 50, 700, 76, 85, 92, 73, 101.
Binary Tree
Binary Tree adalah struktur data pohon di mana setiap node memiliki paling banyak dua anak, yang disebut sebagai anak kiri dan anak kanan. Definisi rekursif hanya menggunakan teori himpunan gagasan adalah bahwa (non-kosong) pohon biner adalah tiga (L, S, R), di mana L dan R adalah Binary Tree atau himpunan kosong dan S adalah satu set tunggal. Beberapa penulis memungkinkan pohon biner menjadi himpunan kosong juga.
Jenis-jenis Binary Tree, yaitu:
- Rooted Binary Tree adalah sebuah tree yang berakar di mana setiap simpul paling banyak mempunyai dua anak
- Full Binary Tree (proper binary tree), adalah sebuah tree di mana setiap simpul mempunyai nol atau dua anak.
- Perfect Binary Tree adalah sebuah Full Binary Tree di mana semua daun memiliki kedalaman yang sama.
- Complete Binary Tree di mana semua daunnya memiliki kedalaman n atau n-1 untuk beberapa n. Agar sebuah tree dapat menjadi sebuah Complete Binary Tree, semua anak pada tingkat terakhir harus menempati titik terkiri secara teratur, dengan tidak ada titik yang menganggur di antara keduanya.
- Almost Complete Binary Tree sebuah tree dimana setiap simpul yang mempunyai anak kanan juga memiliki anak kiri. Memiliki anak kiri tidak memerlukan sebuah simpul untuk mempunyai anak kanan.
Sumber:

Comments
Post a Comment